
在高精度制造领域,优化加工参数的能力是生产成功的关键因素。理解并运用加工经济学原理可以显著降低生产成本和时间,同时提高刀具利用率和制造产量。
本文探讨了一个用于优化加工工艺的综合框架。从初始材料选择到进给速率调整和成本建模,每个阶段都有助于降低成本或提高生产率。目标是为工程师、生产规划人员和机械师提供基于数据和实际生产约束的实用策略。
1.0机械加工经济学简介
加工经济学的核心在于优化加工操作,以实现以下两个目标之一:
- 最大化生产率(即最小化周期时间),或
- 尽量降低生产成本(即实现经济效率)
实现任何一个目标都需要对几个关键决策点采取结构化的方法,包括:
- 起始原料的选择
- 操作规划和工具选择
- 进给率和切削速度优化
- 刀具磨损建模
- 批量生产的成本和时间分析
通过对这些阶段进行建模和优化,制造商可以提高盈利能力、提高资产利用率,并在航空航天、汽车、模具和精密部件等领域获得竞争优势。
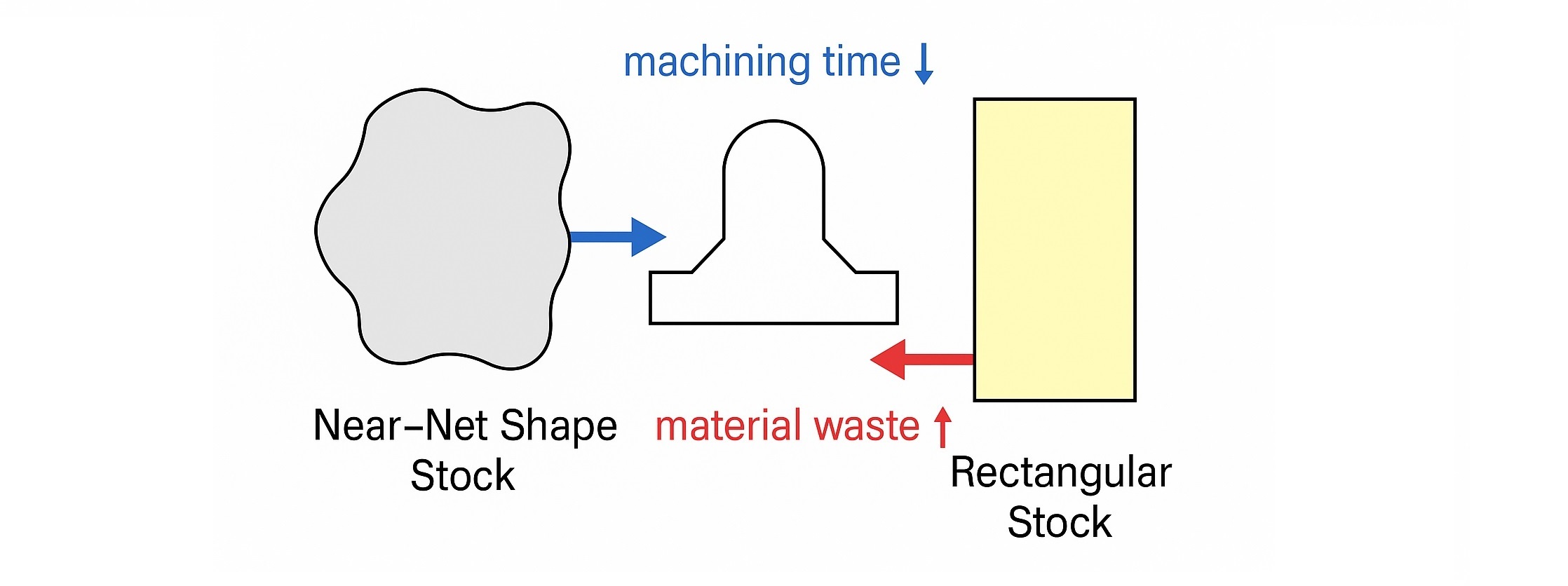
2.0库存选择:近净形状与标准矩形库存
在任何加工操作开始之前,原材料的选择都会对成本和时间产生重大影响。
2.1近净形坯料
近净成形是指与零件最终几何形状紧密匹配的材料。
- 优势:
- 显著缩短加工时间
- 产生更少的废料
- 需要更少的通行证和工具
- 缺点:
- 由于定制铸造或成型,成本通常较高
- 可能需要更长的交货时间
当周期时间至关重要或使用昂贵或难以加工的材料(例如钛合金)时,此选项是理想的选择。
2.2矩形库存(例如,模座块)
矩形库存在通用加工中最为常见,具有成本和可用性优势。
- 优势:
- 广泛可用且成本相对较低
- 标准化尺寸和公差
- 缺点:
- 需要去除更多的材料
- 增加刀具磨损和加工时间
关键策略:务必选择能够安全容纳最终零件的最小库存尺寸。过大的库存会增加浪费和能源消耗,且不会增加价值。
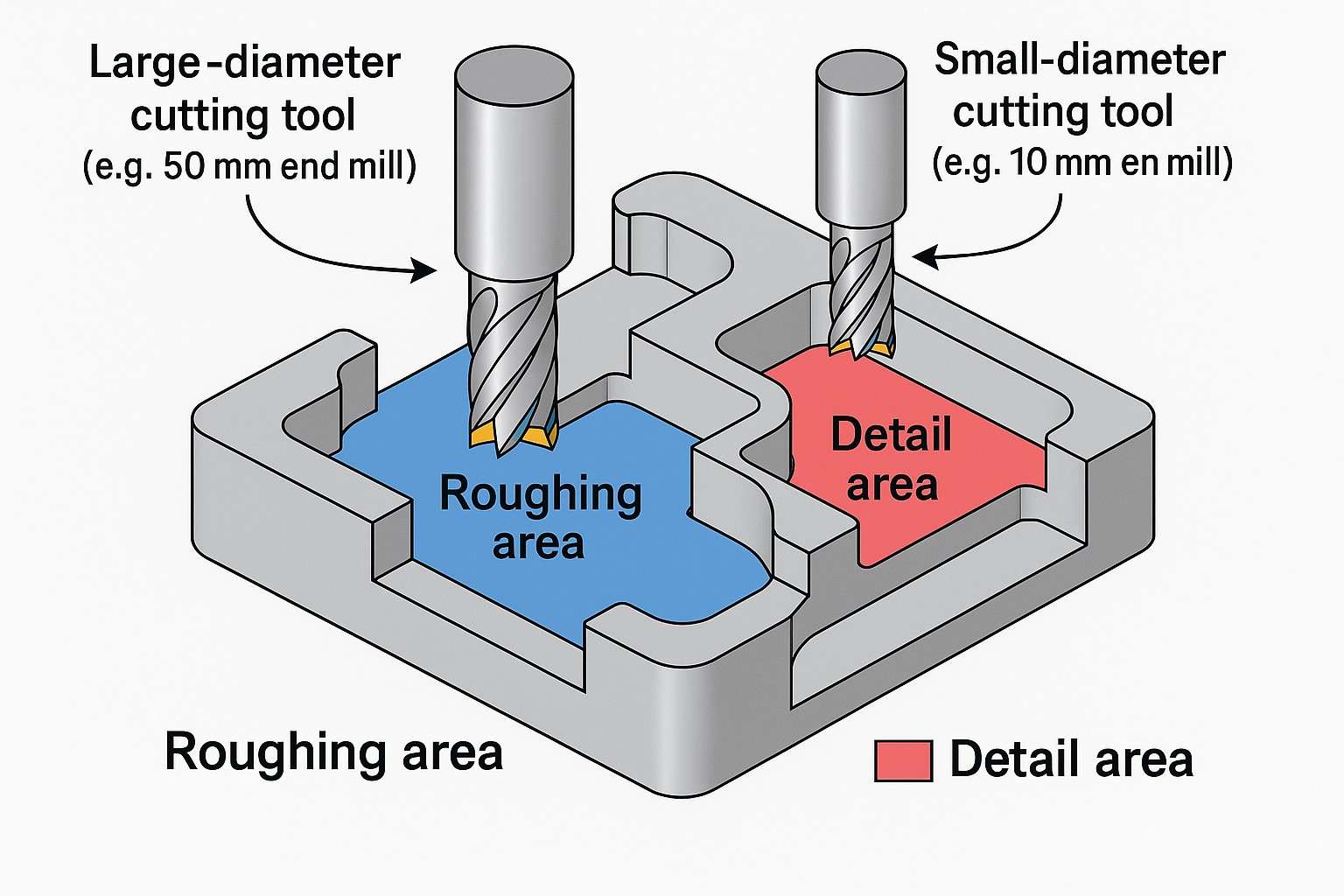
3.0作业规划与工具选择
材料去除率 (MRR) 是衡量加工生产率的基本指标。选择合适的刀具并定义加工区域会直接影响 MRR 和整体效率。
3.1刀具直径和特征尺寸
- 大型工具 是粗加工操作中批量去除和高 MRR 的首选。
- 小工具 对于复杂的特征、紧密的半径或精加工过程是必要的。
建议做法:将零件分解为基于特征的子区域。为每个区域分配合适的最大刀具,确保在保持精度的同时实现最高的去除率。
这种方法最大限度地减少了刀具更换,减少了加工时间,并提高了刀具路径效率。
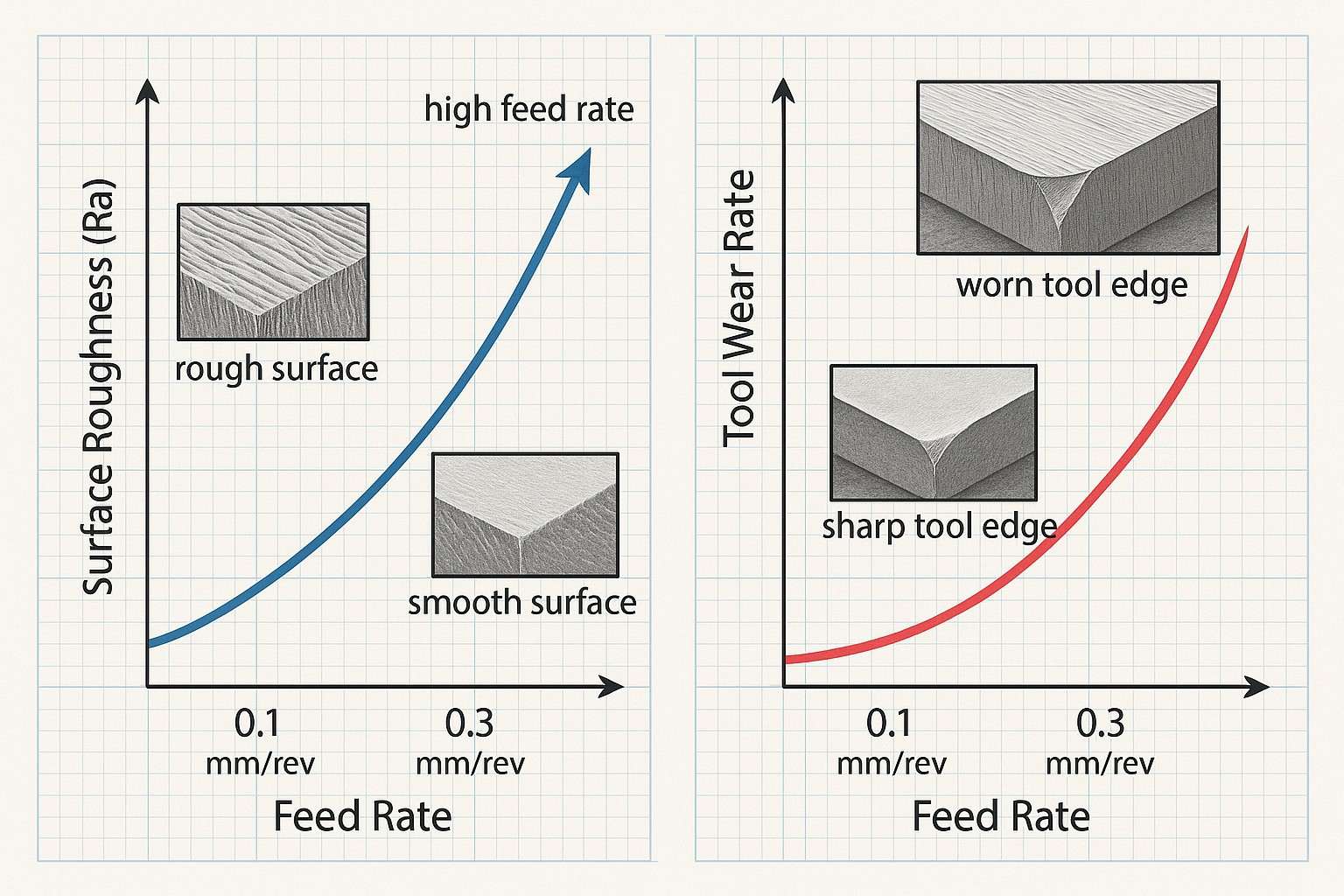
4.0进给率优化:粗加工与精加工
进给率直接影响材料去除率、表面质量、刀具寿命和切削力。
4.1精加工操作
- 更高的进给率 提高生产率但降低表面光洁度。
- 最佳进料速率是 最高值 仍能满足表面质量要求,这取决于:
- 功能公差
- 美学或美容标准
- 适合和装配标准
- 抛光或涂层等后处理操作
4.2粗加工工序
由于接下来会进行精加工,因此表面光洁度不太重要。这里的重点是通过以下方式最大化MRR:
-
更高的切削速度(V)
-
更高的进给率(f)
然而,增加 V 和 f 也会提高刀具温度,进而影响磨损和刀具寿命。
-
切削速度增加切屑速度
-
进给率增加切屑的横截面积
4.3刀具力和功率考虑
-
切削力 与进给速率成比例
-
更高的力量需要:
-
更大的机器功率
-
额定切削负荷更高的工具
-
优化指南:最佳粗加工进给率是满足下列条件的最高值:
- 这 机器的功率容量
- 这 刀具最大切削力极限 (按照制造商的规定)
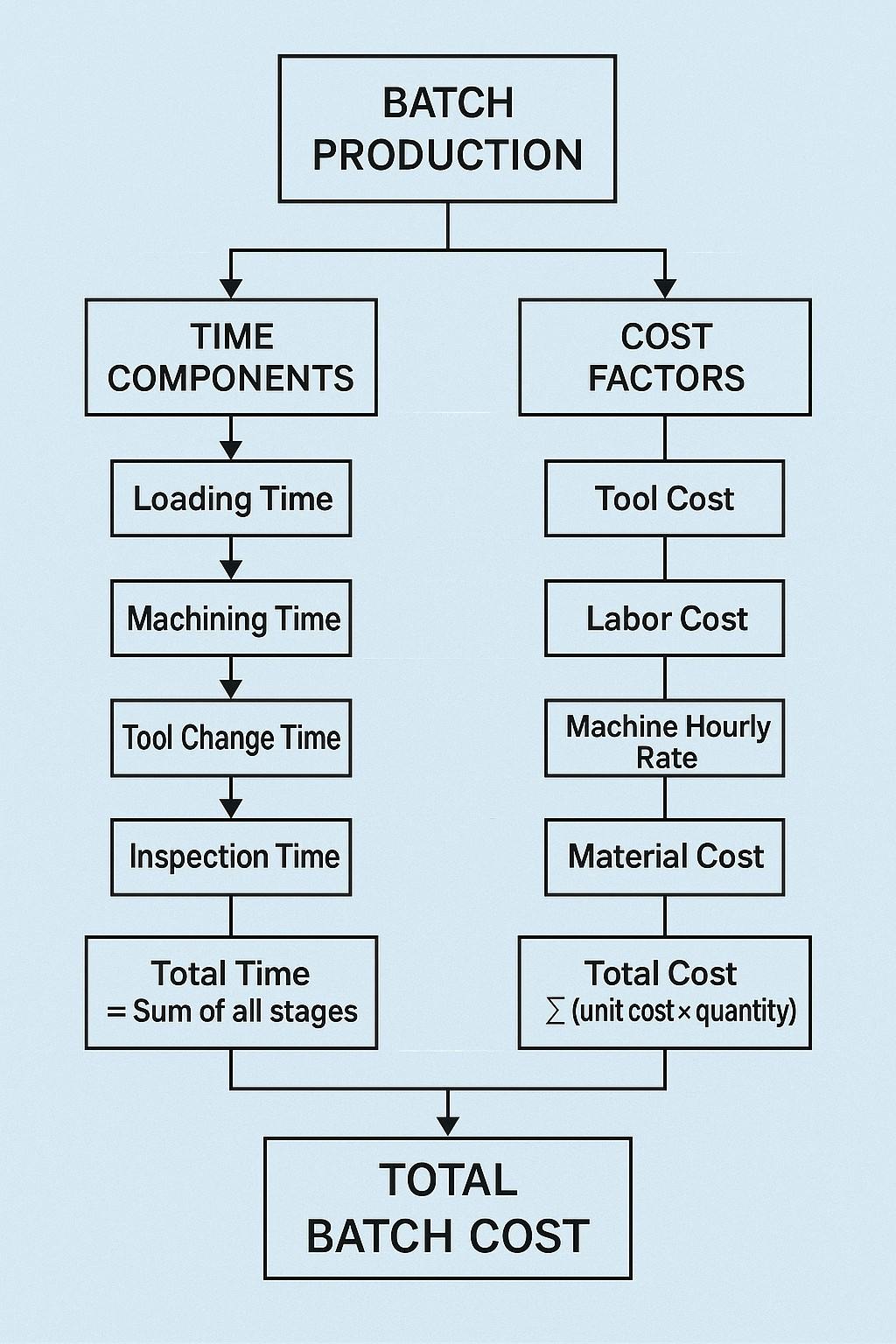
5.0批量生产中的生产成本建模
在批量生产中,总单位成本受生产性和非生产性操作的影响。
假设一批 铌 生产相同的零件。时间和成本构成如下:
5.1时间组件
-
非生产时间 tlt_l:包括装载、设置和卸载。
总非生产时间= Nb⋅tlN_b \cdot t_l -
加工时间 tmt_m:加工单个零件的时间。
总加工时间= Nb⋅tmN_b \cdot t_m -
换刀时间 tct_c:更换磨损工具所需的时间。
总计 = Nt⋅tcN_t \cdot t_c, 在哪里 Nt=Nb⋅tmTN_t = \frac{N_b \cdot t_m}{T}
5.2成本构成
-
CtC_t: 每件工具的成本
-
毫米:每分钟机器和人工成本
每个零件的平均成本模型如下:
$$
C_{pr}(V) = t_l \cdot M + t_m \cdot M + \frac{C_t \cdot t_m}{T} + \frac{t_c \cdot M \cdot t_m}{T}
$$
这个等式清楚地显示了刀具寿命 TT — 切割速度的函数 — 影响总成本。
6.0刀具磨损和泰勒刀具寿命方程
为了准确优化切削参数,必须建立刀具磨损模型。广泛使用的泰勒刀具寿命方程为:
$$
V \cdot T^n = C
$$
在哪里:
- 维维:切割速度
- TT:刀具寿命
- n,Cn,C:基于刀具-工件材料组合的经验常数
求解刀具寿命:
$$
T = \left( \frac{C}{V} \right)^{1/n}
$$
代入成本模型:
$$
C_{pr}(V) = t_l \cdot M + t_m \cdot M + \frac{C_t \cdot t_m}{T} + \frac{t_c \cdot M \cdot t_m}{T}
$$
这将每个零件的成本定义为切割速度的函数 维维.
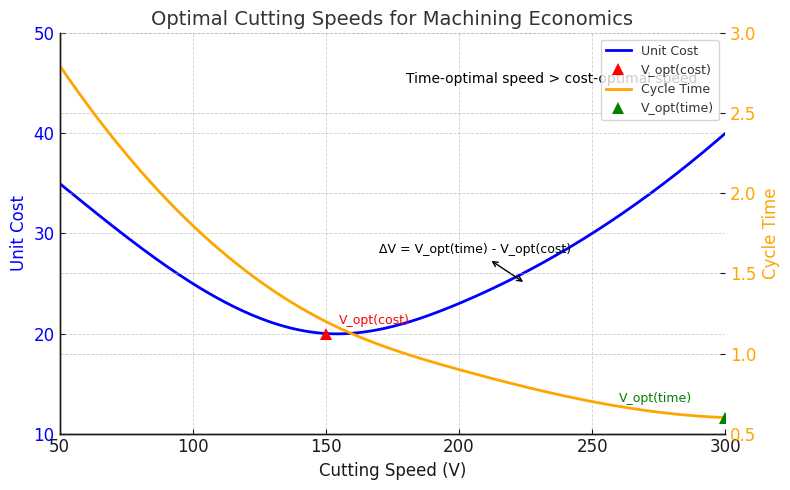
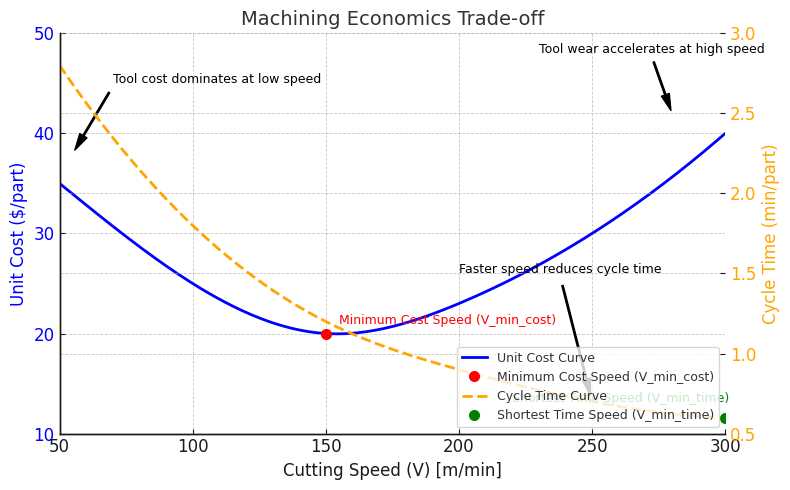
7.0优化切割速度
7.1最低成本的最佳速度
为了最小化单位成本,对切割速度的成本函数进行微分 维维 并将导数设为零:
$$
\frac{d C_{pr}(V)}{dV} = 0
$$
解决这个问题可以得出最低成本的最佳切割速度,表示为:
$$
V_{opt}^{(成本)}
$$
由于较低速度下的刀具寿命更长,因此该速度通常低于最大限度缩短生产时间的速度。
7.2实现最大生产率的最佳速度
每个部分的平均时间建模如下:
$$
T_{avg}(V) = t_l + t_m + \frac{t_c \cdot t_m}{T}
$$
替代 TT,表达式变为 维维. 尽量减少时间:
$$
\frac{d T_{avg}(V)}{dV} = 0
$$
解决这个问题可以得出最短时间内最佳速度:
$$
V_{opt}^{(时间)}
$$
通常,
$$
V_{opt}^{(时间)} > V_{opt}^{(成本)}
$$
因为更高的速度会缩短循环时间但会增加工具消耗。
8.0摘要和实用指南
关键要点:
- 材料选择:在成本允许的情况下,使用近净形状来减少加工时间;否则,优化标准库存尺寸以减少浪费。
- 工具策略:按特征尺寸对零件进行分割,并在每个区域使用最大的允许工具来最大化 MRR。
- 进给速率调节:
- 对于精加工:设置满足表面质量的最高进给。
- 对于粗加工:将进给推至机床功率和刀具能力的极限。
- 切削速度优化:
- 使用泰勒方程来模拟刀具磨损。
- 根据您的目标优化速度:降低成本与加快吞吐量。
- 批量生产经济学:
- 考虑换刀时间、刀具成本和非生产性操作。
- 使用成本模型来选择平衡长期效率的切割速度。
9.0结束语
加工经济学提供了一种结构化的定量方法,可改善 CNC 和手动加工环境中的决策。无论您的目标是成本领先还是高速生产,将这些原则融入 CAM 编程、刀具选择和工艺规划中,都能显著提升效率和盈利能力。


